Towers of Hanoi can be easily implemented using recursion. Objective of the problem is moving a collection of N disks of decreasing size from one pillar to another pillar. The movement of the disk is restricted by the following rules.

Rule 1 : Only one disk could be moved at a time.

Rule 2 : No larger disk could ever reside on a pillar on top of a smaller disk.

Rule 3 : A 3rd pillar could be used as an intermediate to store one or more disks, while they were being moved from source to destination.

Initial Setup of Tower of Hanoi

Tower 1 A

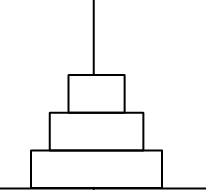
Tower 2 B

Tower 3 C

Recursive Solution

N – represents the number of disks.

Step 1. If N = 1, move the disk from A to C.

Step 2. If N = 2, move the 1^st disk from A to B. Then move the 2^nd disk from A to C, The move the 1^st disk from B to C.

Step 3. If N = 3, Repeat the step (2) to more the first 2 disks from A to B using C  as intermediate. Then the 3^rd disk is moved from A to C. Then repeat the step (2) to move 2 disks from B to C using A as intermediate.

In general, to move N disks. Apply the recursive technique to move N – 1 disks from A to B using C as an intermediate. Then move the N^th disk from A to C. Then again apply the recursive technique to move N – 1 disks from B to C using A as an intermediate

Recursive Routine for Towers of Hanoi

void hanoi (int n, char s, char d, char i)

{

/* n     no. of disks, s    source, d    destination i    intermediate

*/ if (n = = 1)

{

print (s, d); return;

}

else

{

hanoi (n – 1, s, i, d); print (s, d)

hanoi (n-1, i, d, s); return;

}

}

Source Pillar Intermediate Pillar Destination Pillar

1 .Move Tower1 to Tower3

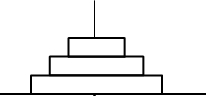
Tower 1

Tower 2

Tower 3

2.Move Tower1 to Tower2

Tower 1

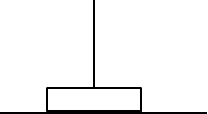
Tower 2

Tower 3

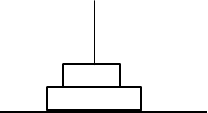
3.Move Tower 3 to Tower 2

Tower 1                                          Tower 2                                Tower 3

4.Move Tower 1 to Tower 3

Tower 1

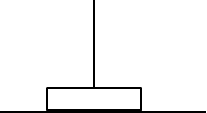
Tower 2

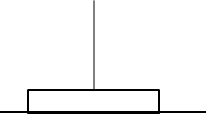
Tower 3

5.Move Tower 2 to Tower 3

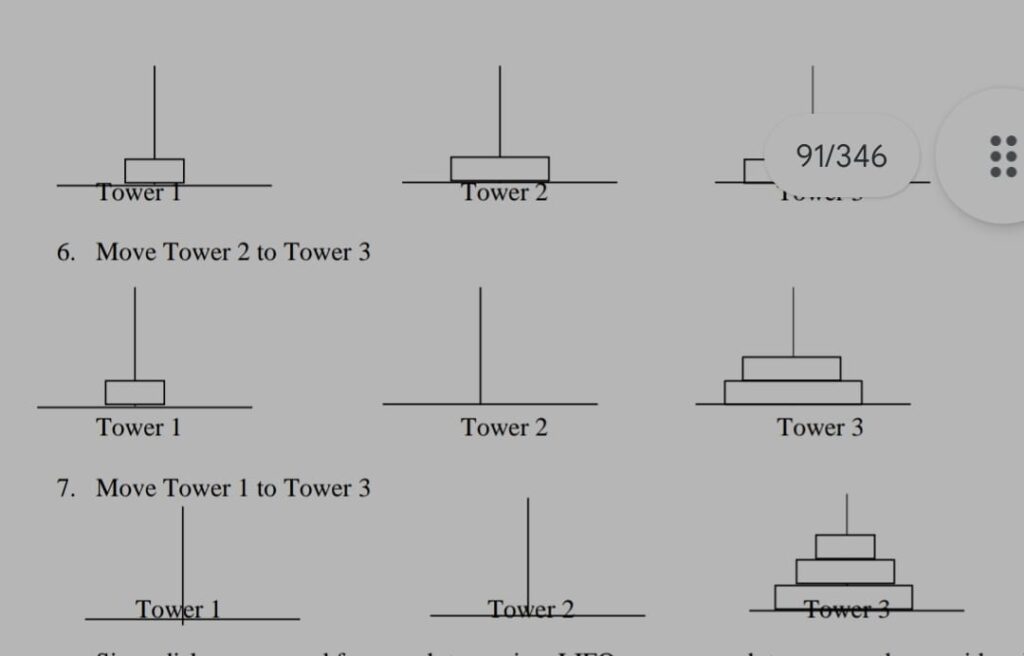
Since disks are moved from each tower in a LIFO manner, each tower may be considered as a Stack. Least Number of moves required solving the problem according to our algorithm is given by,

O(N)=O(N-1)+1+O(N-1) =2^N-1

Other Courses

Cloud Computing

Power BI

NoSQL