There are 3 types of Expressions
- Infix Expression
- Postfix Expression
- Prefix Expression
INFIX
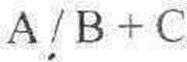
The arithmetic operator appears between the two operands to which it is being applied.
POSTFIX
The arithmetic operator appears directly after the two operands to which it applies. Also called reverse polish notation
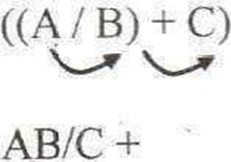
PREFIX
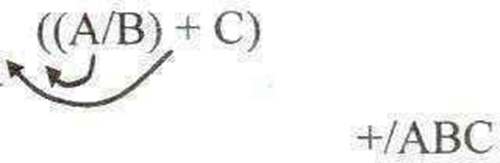
The arithmetic operator is placed before the two operands to which it applies. Also called polish notation.
Evaluating Arithmetic Expressions
- Convert the given infix expression to Postfix expression
- Evaluate the postfix expression using stack.
Algorithm to convert Infix Expression to Postfix Expression:
Read the infix expression one character at a time until it encounters the delimiter “#”
Step 1: If the character is an operand, place it on the output.
Step 2: If the character is an operator, push it onto the stack. If the stack operator has a higher or equal priority than input operator then pop that operator from the stack and place it onto the output.
Step 3:If the character is left parenthesis, push it onto the stack
Step 4:If the character is a right parenthesis, pop all the operators from the stack till it encounters left parenthesis, discard both the parenthesis in the output.
E.g. Consider the following Infix expression: – A*B+(C-D/E)#
| Read char | Stack | Output |
| A | A | |
| * | * | A |
| B | + * | AB |
| + | + | AB* |
| ( | ( + | AB* |
| / – ( + |
Read char
C
–
D
/
E
)
Stack
| ( |
| + |
| – |
| ( |
| + |
| – |
| ( |
| + |
| / |
| – |
| ( |
| + |
| / |
| – |
| ( |
| + |
Output
AB*C
AB*C
AB*CD
AB*CD
AB*CDE
AB*CDE/-
| Read char | Stack | Output |
| # | AB*CDE/-+ |
Algorithm to evaluate the obtained Postfix Expression
Read the postfix expression one character at a time until it encounters the delimiter „#‟ Step 1: If the character is an operand, push its associated value onto the stack.
Step 2: If the character is an operator, POP two values from the stack, apply the operator to them and push the result onto the stack.
E.g consider the obtained Postfix expression:- AB*CDE/-+
Operand Value
A 2
B 3
C 4
D 4
E 2
Char Read Stack
A 2
B 3 2
Char Read Stack
* 6
C 4 6
D 4 4 6
E
/ 2 4 6
– 2 6
+ 8
OUTPUT = 8
Example 2: Infix expression:- (a+b)*c/d+e/f#
Read char Stack Output
( (
a ( a
+ +( a
b +( ab
( ab+
* ab+
ab+c*
#
Postfix expression:- ab+c*d/ef/+
Evaluating the Postfix Expression
| Operand Value |
| a 1 |
| b 2 |
| c 4 |
| d 2 |
| e 6 |
| f 3 |
| Infix to Postfix Conversion | Output |
| #define SIZE 50 /* Size of Stack */ #include <ctype.h> char s[SIZE]; int top=-1; /* Global declarations */ void push(char elem) { s[++top]=elem; } char pop() { return(s[top–]); } int pr(char elem) { /* Function for precedence */ switch(elem) { case ‘#’: return 0; case ‘(‘: return 1; case ‘+’: case ‘-‘: return 2; case ‘*’: case ‘/’: return 3; } return 0; } Void main() { /* Main Program */ char infx[50],pofx[50],ch,elem; int i=0,k=0; printf(“\nRead the Infix Expression ? “); scanf(“%s”,infx); push(‘#’); while( (ch=infx[i++]) != ‘\0‘) { if( ch == ‘(‘) push(ch); else if(isalnum(ch)) pofx[k++]=ch; else if( ch == ‘)’) { while( s[top] != ‘(‘) pofx[k++]=pop(); elem=pop(); /* Remove */ } else { /* Operator */ while( pr(s[top]) >= pr(ch) ) pofx[k++]=pop(); push(ch); } } while( s[top] != ‘#’) /* Pop from stack till empty pofx[k++]=pop(); pofx[k]=’\0‘; /* Make pofx as valid string */ printf(“\n\nGiven Infix Expn: %s Postfix Expn: %s\n“,infx,pofx); } | Read the Infix Expression ? (a+b)-(c-d) Given Infix Expn: (a+b)*(c-d) Postfix Expn: ab+cd-* |
