- In a circular linked list organization, insertion of a record involves modification of
- One pointer
- Two pointers
- Three pointers
- No pointer
[B] Suppose we want to insert node A to which we have pointer p , after pointer q then we will Have following pointer operations
1.p->next=q->next;
2.q->next = p;
So we have to do two pointer modifications
2.Consider a singly linked list having n nodes. The data items d1, d2, …., dn are stored in the n nodes. Let Y be a pointer to the jth node (1 ≤ j ≤ n) in which dj is stored. A new data item d stored in a node with address Y is to be inserted. Give an algorithm to insert d into the list to obtain a list having items d1, d2, ……, dj-1, d, dj, …..dn in that order without using the header.
Algorithm 1 insert_mid( ) 1: create newnode
2: newnode->next=y->next
3: newnode->data=y->data /*which is dj*/
4: y->next=newnode
5: y->data=d
Explanation:
Since we didn’t have the address of node which is previous to Y. So insert a new node after Y.
And copy the data of Y to new node and modify data field of Y to d. Hence we get required sequence of data as d1,d2,…,dj-1,d,dj,…dn
3.Linked lists are not suitable for data structures for which one of the following problems?
A. Insertion sort
B. Binary search
C. Radix sort
D. Polynomial manipulation
[B] For binary search, if we are using array, then we can go to middle of array by just dividing index of array by 2. Since array is stored in contiguous memory. But that is not true in case of linked list. If you want to access middle of list then each time you have to traverse from its head. Hence use of linked list is not good idea for binary search.
4.The concatenation of two lists is to be performed in O(1) time. Which of the following implementations of a list should be used?
(A) singly linked list (B) doubly linked list
(C) circular doubly linked list (D) array implementation of list
[C} For merging of list you have to point next pointer of last node of first list to first node of 2nd list. To do this in O(1) time circular double list is useful. You can go to last node 1st list by head1->next->previous. And modify this field pointing to head2->next. And also modify head2->next->previous to head1->next.
5.(a) Let p be a pointer as shown in the figure in a singly linked list.

What do the following assignment statements achieve?
q: = p→ next
p → next: = q→ next
q → next: = (q → next) → next (p → next) →next: = q
5a)
Que Ans
q: = p→ next cell i->cell (i+1) ->cell(i+2)->cell(i+3) p->cell i,q->cell(i+1)
p → next: = q→ next cell i->cell(i+2)->cell(i+3) & cell(i+1) ->cell(i+2)->cell(i+3)
q → next: = (q → next) → next cell i->cell(i+2)->cell(i+3) & cell(i+1)->cell(i+3) (p → next) →next: = q cell->i->cell(i+2)->cell(i+1)->cell(i+3)
Write a constant time algorithm to insert a node with data D just before the node with address p of a singly linked list.
Constant time algorithm is
Insert before(p)
{
n =newnode();
n->next = p->next; p->next =n
n->data=p->data; p->data = D;
}
As we can’t actually insert before any node to with we have a pointer in singly linked list.
So idea is to insert a node after p , copy the data of p in new node and copy new data in node p.
6.In the worst case, the number of comparisons needed to search a singly linked list of length n for a given element is
- log2n
- n/2
- log2n – 1
- n
[D] In worst case the element is in last node. So we require n comparisons in worst case.
7.In a circular linked list organization, insertion of a record involves modification of
- One pointer
- Two pointers
- Three pointers
- No pointer
[B] Suppose we want to insert node A to which we have pointer p , after pointer q then we will Have following pointer operations
1.p->next=q->next;
2.q->next = p;
So we have to do two pointer modifications
8.Consider a singly linked list having n nodes. The data items d1, d2, …., dn are stored in the n nodes. Let Y be a pointer to the jth node (1 ≤ j ≤ n) in which dj is stored. A new data item d stored in a node with address Y is to be inserted. Give an algorithm to insert d into the list to obtain a list having items d1, d2, ……, dj-1, d, dj, …..dn in that order without using the header.
Algorithm 1 insert_mid( ) 1: create newnode
2: newnode->next=y->next
3: newnode->data=y->data /*which is dj*/ 4: y->next=newnode
5: y->data=d
Explanation:
Since we didn’t have the address of node which is previous to Y. So insert a new node after Y.
And copy the data of Y to new node and modify data field of Y to d. Hence we get required sequence of data as d1,d2,…,dj-1,d,dj,…dn
9.The following C function takes a singly-linked list of integers as a parameter and rearranges the elements of the list. The function is called with the list containing the integers 1,2,3,4,5,6,7 in the given order. What will be the contents of the list after the function completes execution?
struct node { int value;
struct node *next;
};
void rearrange (struct node *list) { struct node *p, *q;
int temp;
if (!list || !list -> next) return; p = list; q = list -> next; while (q) {
temp = p -> value; p -> value =q -> value; q -> value = temp; p = q -> next;
| } (A) 1,2,3,4,5,6,7 (B) 2,1,4,3,6,5,7 (C) 1,3,2,5,4,7,6 (D) 2,3,4,5,6,7,1 |
q = p ? -> next : 0;
}
[B] The q pointer always point to next node of p. And here p is modified first. So swapping is done
10.The data blocks of a very large file in the Unix file system are allocated using
A. contiguous allocation
B. linked allocation
c. indexed allocation
D. an extension of indexed allocation
[D] The file’s inode contains pointer to first 10 data blocks.The 11th pointer in inode points at an indirect block that contain 128 data blocks. And so on…
11.The following C function takes a singly linked list of integers as a parameter and rearranges the elements of the list. The list is represented as pointer to structure. The function is called with the list containing integers 1, 2, 3, 4, 5, 6, 7 in the given order. What will be the contents of the list after the function completes?
struct node {int value; struct node *next;};
void rearrange(struct node *list) { struct node *p, *q;
int temp;
if(!list || !list → next) return; p = list; q = list → next; while(q) {
temp = p → value;
p → value = q → value;
q → value = temp;
p = q → next;
q = p? p → next : 0;
}
}
(A) 1, 2, 3, 4, 5, 6, 7 (B) 2, 1, 4, 3, 6, 5, 7
(C) 1, 3, 2, 5, 4, 7, 6 (D) 2, 3, 4, 5, 6, 7, 1
[B] The q pointer always point to next node of p. And here p is modified first. So swapping is done only once for each
12.Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst case time complexity of the best-known algorithm to delete the node x from the list?
- O(n)
- O(log2 n)
- O(log n)
- O(1)
- As Q is pointing to node X.
So the following algorithm will delete the node in O(1) Algorithm-:
Delete()
Step1. Q->data =: (Q->next)->data
Step2. temp =: Q->next (temp is temporary pointer variable of type list ) Step3. Q->next =: (Q->next)->next
Step4. delete temp
13.Suppose each set is represented as a linked list with elements in arbitrary order. Which of the operations among union, intersection, membership, and cardinality will be the slowest?
A. Union only
B. intersection, membership
C. membership, cardinality
D. union, intersection
[D] For intersection n*n comparisons are required.
For union, just merging of two list will not work. We have to find out common elements which require again n*n comparisons.
For membership only n comparisons are needed.
For Cardinality n comparisons. (ie. For each node check next !=NULL and increment )
14. Circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should p point such that both the operations enQueue and deQueue can be performed in constant time?
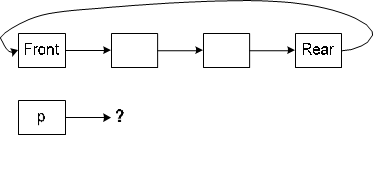
A. Rear node
B. Front node
C. Not possible with a single pointer
D. Node next to front
- p points to rear node
For enQueue
1: create newnode
2: newnode->next=p->next /*which is front node*/ 3: p->next=newnode
4: /*rear=newnode;*/
5: p=rear
For deQueue
1:temp=p->next /*temp is pointing to front node
2: p->next=p->next->next 3:/* front=p->next*/ 4:delete(temp)
